Закон Кеплера известен всем, кто интересуется астрономией и космосом. Он является одним из фундаментальных законов, описывающих движение планет вокруг Солнца. Закон Кеплера был сформулирован итальянским астрономом Иоганном Кеплером в начале 17 века и с тех пор стал основой для понимания многих небесных явлений.
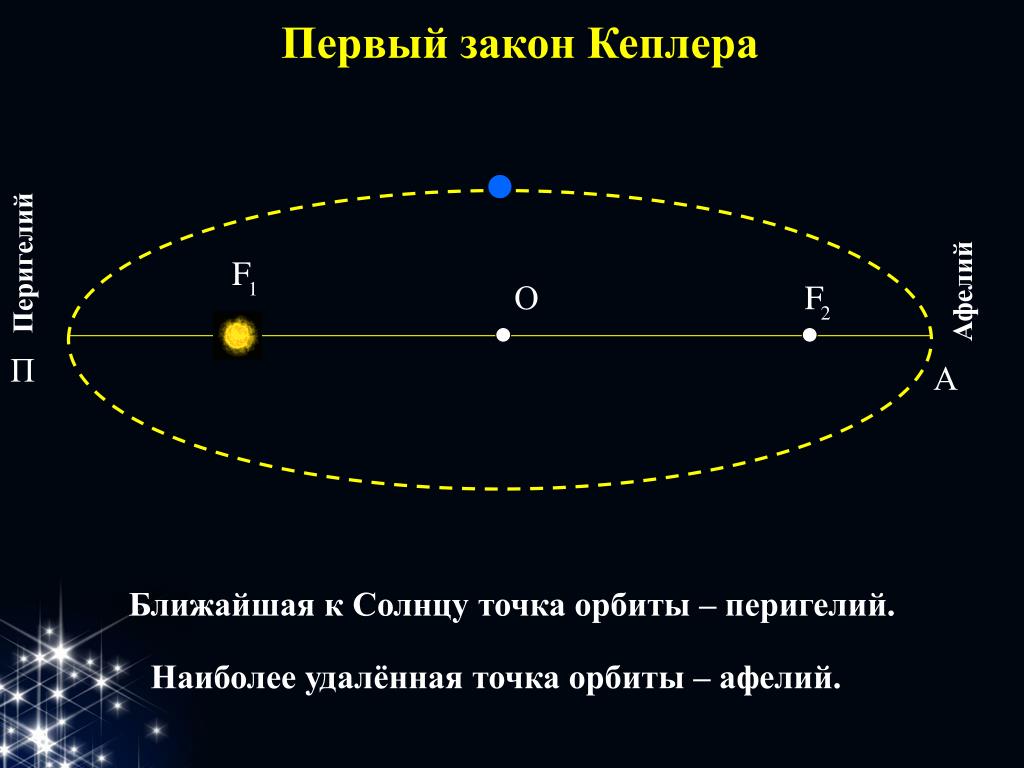
Первый закон Кеплера, или закон орбит, гласит, что планеты движутся по эллиптическим орбитам вокруг Солнца, при этом Солнце находится в одном из фокусов эллипса. Иными словами, траектории планеты являются легко вытянутыми окружностями, описывающими эллипс. Этот закон представляет собой революционное открытие, поскольку предыдущие представления о движении планет считали орбиты идеальными окружностями.
Также Закон Кеплера включает в себя второй закон, или закон радиус-векторов. Он говорит о том, что радиус-векторы, соединяющие Солнце и планеты, за равные промежутки времени равными площадями. Иными словами, скорость планеты вращается по орбите таким образом, что она проводит равные площади за равные промежутки времени. Это означает, что планета движется быстрее в перигелии (точке орбиты, ближайшей к Солнцу) и медленнее в афелии (точке орбиты, самой удаленной от Солнца).
Первый закон Кеплера: закон орбит
Первый закон Кеплера, также известный как закон орбит, был сформулирован Иоганном Кеплером в начале 17 века. Согласно этому закону, все планеты движутся по эллиптическим орбитам вокруг Солнца, которое занимает один из фокусов этих орбит.
Афелий – это точка на орбите, наиболее удаленная от Солнца, а перигелий – точка наиближайшая к Солнцу. Из-за эллиптической формы орбиты, расстояние от планеты до Солнца не является постоянным: оно меняется в зависимости от положения планеты на орбите.
Закон орбит сыграл важную роль в развитии астрономии и позволил Кеплеру создать свои два последующих закона, описывающих движение планет.
Солнце в фокусе орбиты
Это отличие стало одним из ключевых положений, выведенных Иоганном Кеплером в его законах движения планет. Согласно первому закону Кеплера, орбиты планет имеют форму эллипсов, в одном из фокусов которых расположено Солнце.
Фокусное расстояние между Солнцем и фокусом орбиты позволяет объяснить такие феномены, как изменение скорости движения планет в разных точках орбиты и их неравномерные времена обращения.
Фактически, наличие фокуса в орбитах планет является главным причиной планетарного движения. Солнце в фокусе орбиты «тянет» планеты к себе, создавая вокруг себя вращающуюся гравитационную систему.
Благодаря главному закону Кеплера, сформулированному вторым законом, мы можем описывать движение планет по орбитам с высокой точностью и предсказывать их положение в будущем.
Таким образом, наличие фокуса в орбитальном движении планет является одной из особенностей, которая дает понимание и объяснение их движения вокруг Солнца.
Форма орбиты
Согласно первому закону Кеплера, орбиты планет являются эллиптическими, то есть представляют собой овалы. В фокусе эллипса находится Солнце. При этом один из фокусов эллипса является пустым, а второй фокус находится в Солнце.
Орбиты планет также характеризуются вторым законом Кеплера, который гласит, что радиус-вектор, соединяющий планету и Солнце, за равные промежутки времени описывает равные площади. Это означает, что планета движется быстрее, когда находится ближе к Солнцу, и медленнее, когда находится дальше.
Третий закон Кеплера определяет зависимость между периодом обращения планеты вокруг Солнца и её средним расстоянием до Солнца. Согласно этому закону, квадрат периода обращения планеты пропорционален кубу её расстояния до Солнца. Формула для расчета этой зависимости выглядит следующим образом: T^2 = a^3, где T — период обращения планеты в годах, а — среднее расстояние от планеты до Солнца в астрономических единицах.
Таким образом, форма орбиты является одной из ключевых характеристик движения планет вокруг Солнца и определяется законами Кеплера.
Скорость движения по орбите
Согласно первому закону Кеплера, орбита планеты или спутника является эллиптической, при этом центром эллипса является одно из фокусов. Второй закон Кеплера утверждает, что радиус-вектор, соединяющий планету или спутник с его центральным телом, закрывает за равные промежутки времени равные площади. Скорость движения по орбите не является постоянной, она меняется в зависимости от положения планеты или спутника на орбите.
Наибольшая скорость достигается в перигее — точке орбиты, ближайшей к центральному телу. Здесь планета или спутник движется с наивысшей скоростью. В точке апогея, самой удаленной от центрального тела, скорость достигает своего минимума. В остальных точках орбиты величина скорости находится между минимумом и максимумом.
Скорость движения по орбите является критическим фактором, определяющим множество физических явлений и условий, связанных с движением планет и спутников. Она влияет на орбитальный период, силы гравитационного взаимодействия, а также на различные астрофизические процессы.
Второй закон Кеплера: закон радиус-векторов
Второй закон Кеплера утверждает, что радиус-вектор, проведенный от Солнца до планеты, за равные промежутки времени, охватывает равные площади.
Этот закон называется также законом равных площадей. Он имеет важное значение для понимания движения планет вокруг Солнца.
Другими словами, скорость, с которой планета движется вдоль ее орбиты, не постоянна. Когда планета находится ближе к Солнцу, она движется быстрее, а когда она находится дальше от Солнца, она движется медленнее.
Закон радиус-векторов объясняет, почему планеты проходят равные секторы, или площади, за одинаковые промежутки времени.
Например, если планета перемещается от точки А до точки В за одинаковое время, она охватывает равную площадь внутри сектора АСВ.
Этот закон помогает определить скорость планеты в разных точках орбиты. Благодаря закону радиус-векторов ученые могут предсказывать, как планеты будут двигаться в будущем и прошлом.
Из этого закона следует, что планеты движутся быстрее, когда они приближаются к Солнцу в своих орбитах, и медленнее, когда отдаляются от Солнца. Это суть закона радиус-векторов.
Закон радиус-векторов
Иными словами, скорость планеты в разные моменты времени не постоянна, но вектор, соединяющий Солнце и планету, закрывает равные площади за равные промежутки времени. Для этого закона характерны два основных момента:
- Скорость планеты в различных точках орбиты неравномерна. Чем ближе планета к Солнцу, тем выше её скорость, а чем дальше – тем ниже.
- Линия, соединяющая Солнце и планету, сканирует площади, равные за равные промежутки времени. То есть, когда планета движется ближе к Солнцу, линия будет закрывать более <<удлиненную>> траекторию, а когда планета отдаляется от Солнца, линия будет описывать более <<сжатую>> траекторию.
Закон радиус-векторов подтверждает, что движение планет вокруг Солнца является эллиптическим. Это дает основание для построения математической модели движения планет и определения их орбит.
Скорость радиус-вектора
Скорость радиус-вектора является ключевым понятием в законе Кеплера, который описывает движение планет вокруг Солнца. Второй закон Кеплера утверждает, что скорость радиус-вектора планеты на любом отрезке ее орбиты одинакова, то есть радиус-вектор планеты равный промежутку времени за одинаковые промежутки времени.
Этот закон является следствием закона сохранения момента количества движения и говорит о том, что при движении планет по орбите радиус-вектор меняется, но его скорость остается постоянной. Это объясняет, почему планеты движутся быстрее на ближайших от Солнца участках своей орбиты и медленнее на более удаленных.
Примечание: Выражение «скорость радиус-вектора» также может относиться к скорости, с которой радиус-вектор меняется в пространстве с течением времени. Это понятие широко используется в других областях физики, не только при изучении движения планет.
Движения планет по орбите
- Первый закон Кеплера, известный как закон эллипсов, утверждает, что орбита планеты представляет собой эллипс с Солнцем в одном из фокусов.
- Второй закон Кеплера, или закон радиус-векторов, говорит о том, что радиус-вектор, который соединяет планету с Солнцем, заметает равные площади за равные промежутки времени.
- Третий закон Кеплера, называемый Законом гармонии, устанавливает связь между периодом обращения планеты вокруг своей оси и радиусом ее орбиты. Точнее, квадрат периода обращения планеты пропорционален кубу радиуса ее орбиты.
Следуя этим законам, планеты движутся по орбите, причем их скорости меняются в разных точках орбиты. Например, когда планета находится ближе к Солнцу, она движется быстрее, а когда находится дальше – движение замедляется. Эти законы Кеплера помогли понять и объяснить движение планет и других небесных тел в нашей Солнечной системе.
Третий закон Кеплера: закон периодов
Третий закон Кеплера, также известный как закон периодов, устанавливает связь между периодом обращения планеты вокруг Солнца и её средним расстоянием от Солнца.
Сформулированный Иоганном Кеплером в начале XVII века, третий закон Кеплера гласит следующее:
- Квадрат периода обращения планеты вокруг Солнца пропорционален кубу её среднего расстояния от Солнца.
Третий закон Кеплера является математическим выражением отношения между периодом обращения и средним расстоянием планеты от Солнца. Он формализует принципы, которые Кеплер сформулировал на основе наблюдений Флавиуса Птолемея и Тихо Браге.
Благодаря третьему закону Кеплера была открыта зависимость между периодами обращения планет вокруг Солнца и расстояниями от него. Таким образом, третий закон Кеплера играл ключевую роль в формировании основ современной астрономии и обнаружении закономерностей, которые лежат в основе нашего понимания Солнечной системы.
Вопрос-ответ:
Какие законы сформулировал Кеплер?
Иоганн Кеплер сформулировал три закона движения планет: первый закон, или закон путей, в котором говорится, что все планеты движутся по эллиптическим орбитам с Солнцем в одном из фокусов; второй закон или закон равных площадей, который утверждает, что скорость, с которой планета движется по орбите, постоянна, а путь, пройденный за определенный период времени, равен площади сектора, образованного радиус-вектором и линией, соединяющей планету и Солнце; третий закон или закон периодов, который гласит, что квадраты периодов обращения планет вокруг Солнца пропорциональны кубам больших полуосей их орбит.
Что означает первый закон Кеплера?
Первый закон Кеплера, или закон путей, утверждает, что все планеты движутся по эллиптическим орбитам с Солнцем в одном из фокусов. Эллипс является геометрической фигурой, в которой есть два фокуса, и закон Кеплера указывает, что один из фокусов эллиптической орбиты на пути планеты вокруг Солнца всегда совпадает с Солнцем. Этот закон опровергает предшествующую геоцентрическую модель Вселенной, в которой планеты двигались по круговым орбитам.
Как формулируется второй закон Кеплера?
Второй закон Кеплера, или закон равных площадей, утверждает, что скорость, с которой планета движется по орбите, постоянна, а путь, пройденный за определенный период времени, равен площади сектора, образованного радиус-вектором и линией, соединяющей планету и Солнце. Следовательно, при приближении к Солнцу планета ускоряется, а при удалении замедляется. Этот закон объясняет, почему планеты на орбите проходят разные участки с разной скоростью, но проходят одинаковое расстояние за одно и то же время.
Какие особенности имеет Закон Кеплера?
Закон Кеплера имеет несколько особенностей. Во-первых, он описывает движение планет вокруг Солнца. Во-вторых, он состоит из трех законов. В-третьих, Закон Кеплера основан на наблюдениях и эмпирических данных. И, наконец, этот закон является основой для формулирования законов Ньютона о движении.